Posted by: Leo van Iersel

15Nov / 2020

Rooted phylogenetic networks for coronaviruses

In a previous post, Guido constructed trees for coronaviruses in the SARS group to search for evidence of recombination. He also constructed unrooted data-display networks using SplitsTree. Here, we discuss our attempts to construct rooted genealogical phylogenetic networks for the same dataset [6] but with some modifications.

In particular, we deleted some sequences, giving a smaller data set with only 12 taxa. These taxa include, next to SARS-CoV-2 (the virus causing COVID-19) and SARS-CoV (responsible for the SARS epidemic in 2002/2003), the viruses MP789 and PCoV_GX-P1E sampled from Malayan pangolins from two different Chinese provinces and several viruses found in different bat species in the horseshoe bat genus (Rhinolophus), all from China.

This research was done by Rosanne Wallin, an MSc student at VU Amsterdam and UvA. Her full thesis as well as all data and results can be found on github.

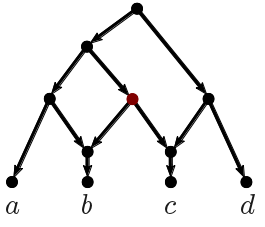
The first algorithm we applied to this data set was the TreeChild Algorithm [1], which is one of the methods that take a number of discordant (rooted, binary) trees as input and finds a rooted network containing each input tree, minimizing the number of reticulate events in the network. To filter out some noise, we contracted some poorly-supported branches and then resolved multifurcations consistently across the trees (using a tool within the TreeChild Algorithm). This gave the network below. Note that the method is restricted to so-called tree-child networks, meaning that certain complex scenarios are excluded (where a network node only has reticulate children). Also note that this is not necessarily the only optimal tree-child network and not all topological differences can be distinguished based on the trees [5].

Figure 1: Phylogenetic network constructed by the Tree-Child algorithm (blocks_A_len0.01_supp70).

The network shows no reticulation in the SARS-CoV-2 clade (the bottom four taxa) and puts SARS-CoV-2 right next to RaTG13. Furthermore, it shows a reticulation between an ancestor of HKU3-1 and a common ancestor of SARS-CoV-2 and RaTG13 leading to bat-SL-CoVZC45. However, it cannot exactly identify which common ancestor of SARS-CoV-2 and RaTG13 is the parent, leading to multiple branches (in red) leading into this reticulation. All these observations are consistent with previous research [2].

Importantly, we cannot directly conclude that each reticulation corresponds to a recombination event. See Table 2.1 of David’s book [10] for a nice overview of possible causes of reticulation. Nevertheless, based on [2], it does look like at least the reticulation leading to bat-SL-CoVZC45 corresponds to a recombination event.

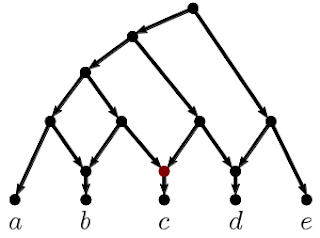
The second algorithm we applied was TriLoNet [3], which constructs a rooted network directly from sequence data. It is restricted to so-called level-1 networks, meaning that it cannot construct overlapping cycles. This method produced the network below.

Figure 2: Phylogenetic network constructed by TriLoNet.

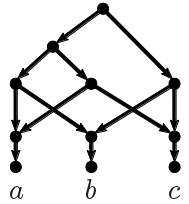
At first sight, the network may look a bit different from the previous one (Figure 1). However, note that the three observations above also hold for this second network. Moreover, the SARS-CoV-2 clade is identical in both networks. This network contains only one reticulation, which is most likely due to the level-1 restriction.

Nevertheless, we can still use this method to find more putative recombination events. To do so, we simply exclude the recombinant bat-SL-CoVZC45 from the analysis and rerun the algorithm. This gives the following network.

Figure 3: Phylogenetic network constructed by TriLoNet, after omitting bat-SL-CoVZC45.

We have now found a second putative recombination event with Rf1 as recombinant. Note that this is also consistent with the network in Figure 1. On the other hand, also note that the branching order in the SARS-CoV clade (the bottom 7 taxa in Figure 3) has changed a bit. This could mean that more recombination events are present in the SARS-CoV clade, as we also see in Figure 1.

One interesting follow-up question is whether the two (or more) networks produced by TriLoNet can be combined into a single higher-level network, in order to show multiple reticulations simultaneously (see [4] for an algorithm that could be useful).

Another interesting observation from these networks is that there is no sign of recombination involving the pangolin coronaviruses MP789 and PCoV_GX-P1E. It rather looks like these viruses evolved from common ancestors of SARS-CoV-2 and RaTG13, but it is important to note that we cannot exclude a recombination event on the basis of these networks. The relationship between SARS-CoV-2 and pangolin coronaviruses is still being debated in the literature [2,7,8,9].

Some limitations of the algorithms were noticed during this study. Firstly, the depicted networks are purely topological, i.e., the branch lengths do not represent anything. Adapting these algorithms to take branch length information into account could possibly improve their accuracy for this data set since the extant taxa have precise time stamps and for recent divergence events these times can be estimated quite accurately, see [2].

Another limitation is that we had to remove several taxa from the original data set [6] before the TreeChild algorithm could find a solution. By removing taxa, we reduced the number of reticulations needed to display the trees, making the TreeChild algorithm run in reasonable time. We made sure to include a diverse set of taxa (based on their pairwise distances [6]) to represent as much of the subgenus as possible. 

Rosanne used several other algorithms, taxon selections and also used trees based on genes rather than fixed-length blocks (which we did above, following Guido’s post), see her thesis on github.

Conclusion
Although rooted phylogenetic network methods are often limited in the number of taxa that can be analysed and/or the complexity of the networks that can be constructed, we have seen that these methods can be useful for constructing hypothetical evolutionary histories. Moreover, although the constructed networks are not identical, we have seen that they share certain key properties, which are also consistent with previous research.  

Rosanne Wallin, Leo van Iersel, Mark Jones, Steven Kelk and Leen Stougie


[1] Leo van Iersel, Remie Janssen, Mark Jones, Yukihiro Murakami and Norbert Zeh. A Practical Fixed-Parameter Algorithm for Constructing Tree-Child Networks from Multiple Binary Trees. arXiv:1907.08474 [cs.DM] (2019).

[2] Maciej F. Boni, Philippe Lemey, Xiaowei Jiang, Tommy Tsan-Yuk Lam, Blair W. Perry, Todd A. Castoe, Andrew Rambaut and David L. Robertson. Evolutionary origins of the SARS-CoV-2 sarbecovirus lineage responsible for the COVID-19 pandemic. Nat Microbiol 5, 1408–1417 (2020). https://doi.org/10.1038/s41564-020-0771-4

[3] James Oldman, Taoyang Wu, Leo van Iersel and Vincent Moulton. TriLoNet: Piecing together small networks to reconstruct reticulate evolutionary histories. Molecular Biology and Evolution, 33 (8): 2151-2162 (2016). http://dx.doi.org/10.1093/molbev/msw068 (postprint)

[4] Yukihiro Murakami, Leo van Iersel, Remie Janssen, Mark Jones and Vincent Moulton. Reconstructing Tree-Child Networks from Reticulate-Edge-Deleted Subnetworks. Bulletin of Mathematical Biology, 81(10):3823–3863 (2019).

[5] Fabio Pardi and Celine Scornavacca. Reconstructible phylogenetic networks: do not distinguish the indistinguishable. PLoS Comput Biol, 11(4), e1004135 (2015).

[6] Grimm, Guido; Morrison, David (2020): Harvest and phylogenetic network analysis of SARS virus genomes (CoV-1 and CoV-2). figshare. Dataset. https://doi.org/10.6084/m9.figshare.12046581.v3

[7]  Lam, Tommy Tsan-Yuk, Marcus Ho-Hin Shum, Hua-Chen Zhu, Yi-Gang Tong, Xue-Bing Ni, Yun-Shi Liao, Wei Wei, et al. Identifying SARS-CoV-2 Related Coronaviruses in Malayan Pangolins. Nature, 583, 282–285 (2020). https://doi.org/10.1038/s41586-020-2169-0

[8] Wang, Hongru, Lenore Pipes, and Rasmus Nielsen. Synonymous Mutations and the Molecular Evolution of SARS-Cov-2 Origins. [Preprint] Evolutionary Biology, April 21, 2020. https://doi.org/10.1101/2020.04.20.052019

[9] Li, Xiaojun, Elena E. Giorgi, Manukumar Honnayakanahalli Marichannegowda, Brian Foley, Chuan Xiao, Xiang-Peng Kong, Yue Chen, S. Gnanakaran, Bette Korber, and Feng Gao. Emergence of SARS-CoV-2 through Recombination and Strong Purifying Selection. Science Advances, Vol. 6, no. 27 (2020). https://doi.org/10.1126/sciadv.abb9153 

[10] David Morrison, Introduction to Phylogenetic Networks. RJR Productions, Uppsala, Sweden (2011). http://www.rjr-productions.org/Networks/index.html


Posted by in coronavirus, Evolutionary network, TreeChild Algorithm, TriLoNet, Viruses

Permalink

05Aug / 2015

First millennium problem has been solved: tree containment is easy on stable networks

One of the most fundamental computational problems related to phylogenetic networks is the following Tree Containment problem. Given a phylogenetic network and a phylogenetic tree, does the network display the tree? (Basically meaning that the tree can be obtained from the network by deleting nodes and branches.)

This problem was shown to be NP-hard in this paper in 2008. So, not only is it difficult to reconstruct phylogenetic networks, it is even difficult to check if a given network is consistent with certain gene trees or the estimated species tree.

In this paper in 2010, Charles Semple, Mike Steel and I studied for which classes of networks this problem remains hard and for which ones it becomes easy. In particular, we showed that the problem becomes polynomial-time solvable on so-called binary tree-child networks.

However, we were not able to extend our algorithm to a more general class of networks called reticulation visible networks, which were later called stable networks by others. A network is reticulation visible if, for each reticulation r, there exists a leaf x such that, if one would delete r, there would be no more directed path from the root to x. The idea behind this class of networks is that the leaf x gives us some information about the reticulation r. And how can we possibly expect to reconstruct reticulations if we don't have any information about them? Moreover, the class of reticulation visible networks seems to be much larger than the class of tree-child networks.

We advertised this open problem as Problem 4 in a list of seven important open computational problems related to phylogenetic networks in this blog post. Recently, there has been quite some interest in the problem, and two papers have presented algorithms for restricted subclasses. A solution for the whole class of binary stable networks has now been proposed in:

Andreas D.M. Gunawan, Bhaskar DasGupta, Louxin Zhang. Stability Implies Computational Tractability: Locating a Tree in a Stable Network is Easy. arXiv:1507.02119 [q-bio.PE]

The paper has not been published yet, but the proof seems correct to me, and is very clever and elegant. Hence, the first of the seven "phylogenetic network millennium problems" has been solved!

Below you see Louxin Zhang presenting the algorithm at the Phylogenetic Networks workshop in Singapore.


Posted by in Uncategorized

Permalink

03Aug / 2015

Networks vs augmented trees

The distinction between networks and augmented trees is interesting from a biological, computational and mathematical point of view. An augmented tree is the result of adding cross-connecting branches to a tree, turning it into a network. So each augmented tree is a network (called a tree-based network). But is each network an augmented tree? In a previous blog post we showed that this is not the case. There exist networks that are inherently network-like and cannot be obtained by adding branches to a tree. (If we are allowed to create new nodes by subdividing branches of the tree, but are not allowed to subdivide any of the previously-added branches.)

The biological question here is as follows: is evolution a tree-like process augmented with horizontal events, or is evolutionary inherently network-like?

This concept is also relevant to phylogenetic network reconstruction approaches, because several such methods work by adding edges to an estimated species tree. Therefore, there exist networks that will always be missed by such methods.

Interestingly, it has turned out that it is easy to find out if a given network is tree-based or not. A polynomial-time algorithm was presented recently by Francis and Steel:

Andrew Francis and Mike Steel, Which Phylogenetic Networks are Merely Trees with Additional Arcs? Systematic Biology (2015).

They solve the problem by reducing it to a model called 2-SAT, which is interesting because it automatically leads to a very simple and fast algorithm solving the problem.

An interesting question that remains open is the following. Given a network and a tree, can we decide in polynomial time if the network can be obtained by adding edges to the given tree? Another question is whether there exists a clean graph-theoretic characterisation of tree-based networks.

Below you see Mike Steel presenting their recent paper at the Phylogenetic Networks Workshop in Singapore. He also discussed other recent results, concerning folding and unfolding phylogenetic trees and networks, as well as distance-based methods for detecting reticulation.


Posted by in Uncategorized

Permalink

16Jul / 2014

Touching the Data, photos

We all worked hard during the workshop. Here is our fearless leader, in deep thought:


While some of the younger participants enjoyed drawing on the walls:


Professor Whitfield has come up with a great new model of evolution: phylogenetic windmills:



There was not only work, but also time to relax and enjoy the beautiful Dutch summer weather:


And not to forget the delicious Dutch food:


But really, most of the time we were busy touching the data, which you can find on this website:


For more photos, see the Touching the Data website.

Posted by in Uncategorized

Permalink

28Jun / 2014

Phylogenetic network Millennium problems


It was 14 years ago that the Millennium started, but there are therefore still 986 years left to solve the following seven phylogenetic network Millennium problems. These are not necessarily the most important problems to solve from a biological point of view, but are challenging computational problems that have (at least) some biological relevance. The problems are all about phylogenetic networks, except for Problems 2 and 7 which are about the closely related topic of agreement forests. Solving these problems will not be rewarded with $1,000,000 but only with eternal fame.

In each of these problems, a phylogenetic network on X is a directed acyclic graph with a single root and no vertices that have only one incoming and only one outgoing arc, and in which each leaf is labelled by an element of X and each element of X labels one leaf.

Problem 1. Is the Hybridization Number problem fixed-parameter tractable (FPT) if the input is an unrestricted set of nonbinary trees and the only parameter is the hybridization number? Hybridization Number is the following problem. Given a finite set X, a collection T of rooted (possibly nonbinary) phylogenetic trees on X and a natural number k, decide if there exists a rooted phylogenetic network on X that displays all trees from T and has reticulation number at most k. See e.g. (van Iersel, Kelk, 2013) for more detailed definitions.

Problem 2. Does there exist a polynomial-time 2-approximation algorithm for MAF on two binary trees? Maximum Agreement Forest (MAF) on two binary trees can be defined as follows. Given a finite set X and two rooted binary phylogenetic trees on X, what is the minimum number number of components in a forest on X that can be obtained from each of the input trees by deleting vertices, deleting edges and suppressing indegree-1 outdegree-1 vertices? For a 2.5-approximation see (Shi, You, Feng, 2014).

Problem 3. Is there an FPT algorithm for finding a level-k phylogenetic network consistent with a given dense set of rooted triplets, if k is the parameter? A rooted triplet is a phylogenetic tree with three leaves. A set of rooted triplets is called dense if it contains at least one triplet for each combination of three leaves. A network is level-k if it can be turned into a tree by deleting at most k edges per biconnected component. This problem is known to be solvable in polynomial time if k is fixed, see (Habib and To 2012).

Problem 4. Is Tree Containment polynomial-time solvable or NP-hard for reticulation visible networks? Tree Containment is the problem of deciding if a given phylogenetic network displays a given tree. A phylogenetic network is called reticulation visible if from each reticulation (vertex with indegree greater than one) there exists a path that does not pass through any other reticulations and ends in a leaf. Tree Containment is known to be NP-hard for general networks and for some restricted classes of networks; see (Kanj, Nakhleh, Than, Xia, 2008) and (van Iersel, Semple, Steel 2010).

Problem 5. Is there a constant-factor approximation algorithm for computing the softwired parsimony score of a binary tree-child network and a binary character? Given a network and a character state (0 or 1) for each leaf, the softwired parsimony score is the minimum number of state-changes in any tree (on all leaves) displayed by the network, over all possible assignments of states to the internal vertices. A phylogenetic network is called tree-child if each non-leaf vertex has at least one child that is not a reticulation. This problem does not have a constant factor approximation for general networks or for other (less severely) restricted classes of networks, unless P = NP (Fischer, van Iersel, Kelk, Scornavacca 2013).

Problem 6. Given k > 1, what is the maximum value of p such that for any set of rooted triplets there exists some level-k phylogenetic network on n leaves that is consistent with at least a fraction p of the input triplets? For k = 0 the maximum is p = 1/3 and for k = 1 it is roughly 0.48, see (Byrka, Gawrychowski, Huber, Kelk 2009).

Problem 7. Is there an O(c^n) algorithm for Maximum Acyclic Agreement Forest (MAAF) on two binary phylogenetic trees with c < 2? An acyclic agreement forest is an agreement forest (see above) for which the following directed graph D is acyclic. D has a vertex for each component of the forest and there is an arc from component A to component B if in at least one of the input trees there is a directed path from the root of A to the root of B. It is known that there exist an O*(2^n) algorithm for this problem (van Iersel, Kelk, Lekic, Stougie, 2013).

Posted by in combinatorial optimization, open problems

Permalink

30Mar / 2014

Candy Crush network


King Digital, the creators of the popular smartphone game Candy Crush Saga were listed on the New York Stock Exchange two days after this game was shown to be NP-hard [1]. Could these two events be somehow related? Anyway, although the King Digital shares are not doing well, the NP-hardness proof still stands. A different NP-hardness proof for Candy Crush actually appeared on the arXiv a few weeks earlier [2], but was based on rules that are slightly different from the usual rules of Candy Crush.

So what is Candy Crush? It is a smartphone / tablet game having a rectangular board filled with different types of candies. A player can score points by swapping two adjacent candies in order to match three or more candies of the same type. This seems to be even more addictive than eating candies, which made the game the most popular game of Facebook, and led to a 568 million dollar profit for King Digital in 2013.

Interestingly, Candy Crush Saga is one of a large family of games that are all based on matching objects. These games all seem to be closely related. Moreover, their genealogy is not tree-like at all, as shown below. Many modern games have been derived by combining ideas from different older games. In other words, the genealogy of such games can best be described by a phylogenetic network.


A phylogenetic network for Bejeweled-type games, taken from [1], which was in turn taken (after modification) from [3].

This network is clearly a rooted, genealogical phylogenetic network (although it does not have a unique root).

So what does the NP-hardness of Candy Crush tell us? Nothing, of course, except that the 97 million people daily playing Candy Crush are pouring all their energy into solving a frivolous, but nevertheless intrinsically hard, problem. This is a pity because, since Candy Crush is NP-hard, one can (at least in theory) encode any NP-complete problem as a Candy Crush episode. This could be used to let all these 97 million people solve more useful NP-complete problems every day. For example, we could encode massive phylogenetic network reconstruction problems as Candy Crush episodes, and use this to construct the Web of Life in a few days!

References

[1] Luciano Gualà, Stefano Leucci, Emanuele Natale. Bejeweled, Candy Crush and other match-three games are (NP-)hard, http://arxiv.org/abs/1403.5830 (24 March 2014)

[2] Toby Walsh. Candy Crush is NP-hard, http://arxiv.org/abs/1403.1911 (8 March 2014)

[3] Jesper Juul. A casual revolution: reinventing video games and their players. The MIT Press, 2012.


Later note:
It turns out that the figure shown above is not actually taken from [3], in spite of the claim made in [1]. The figure in [3] is re-drawn from [4], and the genealogy as shown in [1] is edited directly from [4], not [3]. The editing consists of deleting all of the many other descendants of Tetris. The original complete figure is available here.

[4] Jesper Juul. Swap adjacent gems to make sets of three: a history of matching tile games. Artifact 1: 205-216, 2007.

Posted by in Candy Crush Saga, games, Genealogy, NP-hard

Permalink

03Mar / 2013

Different topological restrictions of rooted phylogenetic networks. Which make biological sense?


Those readers active in the field of evolutionary phylogenetic networks will know that there are many different definitions of “rooted phylogenetic network” in circulation. While certain features are almost universal (e.g. rooted, acyclicity), many are not. Why do these differences arise? There are multiple answers to this. Some arise because of differing opinions on what biologically realistic is, and (relatedly) what the correct balance is between biological detail and mathematical abstraction. Others arise because they make optimization problems on networks easier to solve. This should not automatically be viewed as mathematics prescribing reality to biology, but rather as the observation that if evolution looks like this then certain optimization problems can be solved well. Finally, some differences are superficial; they do not lead to any intrinsic differences in the model or its underlying mathematical structure. Of course, “superficial” is highly context dependent, as some of the examples below will show.

Here we list some well-known and less-well known properties that have surfaced in definitions of rooted phylogenetic network. We will take as given that evolution is directed i.e. that the arcs in the network have an explicit orientation (representing the flow of time). Below most properties we show a figure of a network violating it.

The question to our readers, particularly those from the biological side of the spectrum: which of the following properties make sense? And which other restrictions would make more sense biologically?

Rooted
A root is a node with indegree 0, meaning that it does not have any ancestors. If evolution is assumed to be acyclic (see below) then there will always be at least one root. Most articles writing about rooted phylogenetic networks assume a single root (which is necessarily an ancestor of every node in the network). Some time ago on this blog David raised the question of whether it would not sometimes be better to allow multiple roots. This is an interesting point both from the perspective of interpretation (what does it mean?) and its impact on algorithmic efficiency.

Acyclic
Most models assume acyclicity: it is not possible to walk along the arcs of the network (respecting their orientation) such that you end up back where you started. The most intuitive argument for this is the passing of time: if arcs represent forward motion through evolutionary time, how can you end up back at an earlier point in time? Recently someone pointed out to me that in the reconciliation literature – where one shows how to reconcile a given gene tree with a given species tree – acyclicity is actually not sacred at all. The reason for this is that, without the acyclicity constraint, the problem becomes computationally tractable. See this recent RECOMB 2013 article [3] for an example of this.

Time-consistent
This is an interesting property. It was introduced to prevent reticulation events between non-contemporaneous taxa. That is, to avoid absurd situations such as an organism hybridizing with its ancestor. The most common mathematical articulation of time-consistency is this: it should be possible to put a “time-stamp” on each node of the network such that (a) time always moves strictly forward along tree-edges , and (b) all the nodes involved in a reticulation event have the same time-stamp. The figure here shows a network that is not time-consistent. For many contextualisations of “reticulation event” time-consistency seems to make a lot of sense. But there is a catch. A network might fail to be time-consistent only for the rather artificial reason that we failed to sample a taxon that was, in fact, part of the network (incomplete taxon sampling). Given the reality of incomplete data, demanding time-consistency might be too prohibitive. However, as with all restrictions in this blog, it is perhaps useful as a selection criterion for preferring one network over another.

Figure 1: A network that is not time-consistent. The red and blue node are the two parents of a reticulation node but cannot have coexisted in time.


Degree-restricted
The indegree of a node is the number of parents of it, and the outdegree of a node is the number of children of it. In a bifurcating, rooted phylogenetic tree all nodes have indegree-1 (except the root: indegree-0) and outdegree-2. Polytomies have outdegree-3 or higher.  In a rooted phylogenetic network we also have reticulation nodes i.e. nodes with indegree-2 or higher. Articles differ in the degree-restrictions they place on nodes; there is an entire zoo of different permutations possible. Many articles agree that nodes with indegree-1 and outdegree-1 should not be allowed, because they are phylogenetically uninformative (and indeed such nodes are also rarely encountered in the phylogenetic tree literature). But what about polytomies? And what about reticulation nodes: should they be permitted to have indegree-3 or higher, and if so how should such “reticulate polytomies” be interpreted? From a parsimony perspective it is usual to argue that reticulate polytomies should be more “expensive” than indegree-2 reticulations, because a single reticulation polytomy can explain far more discordance than a single indegree-2 reticulation. Interestingly, some optimization problems are not really affected at all by degree-restrictions on phylogenetic networks (e.g. the hybridization number problem) while others are highly sensitive to degree-restrictions (e.g. the small parsimony problem).

Tree-child
Every node has at least one non-reticulate child. This restriction makes sure that there are no "invisible nodes", i.e. nodes from which all paths end up in reticulations. As a result, this restriction makes many computational problems more tractable and mathematical reasoning easier. For example, consider the basic Tree Containment problem, i.e. given a phylogenetic network and a phylogenetic tree, decide if the network displays the tree, see [8]. This problem was shown to be tractable for tree-child networks, while it is NP-hard for most other classes of networks (time-consistent, tree-sibling, regular). This seems important because if it is already hard to tell if a given tree is in a given network, then it seems  a daunting task to try to build networks of that class from any kind of data.

It should be noted that there is of course no guarantee that "real" evolutionary histories are tree-child. In fact, simulation studies show that only under very low recombination rates one can expect tree-child networks [1][2].

Figure 2: A network that is not tree-child. The red node does not have a non-reticulate child.

Tree-sibling
Every reticulate node has at least one non-reticulate sibling. Originally introduced by Cardona, Llabrés, Rosselló and Valiente who write "Biologically, this condition means that for each of the reticulation events, at least one of the species involved in it has also some descendant through mutation" and showed that networks can efficiently be compared (with a polynomial-time computable metric) if they are both tree-sibling and time-consistent.

An advantage of the class of tree-sibling networks is that it is much larger than the class of tree-child networks. If a reticulation has no non-reticulate siblings, then its parents have no non-reticulate children. Hence, every tree-child network is tree-sibling. However, it can easily be seen that there are many tree-sibling networks that are not tree-child. Computationally, the tree-sibling restriction does not seem to help as much as the tree-child restriction. Again, there is no guarantee that the "real" network is tree-sibling, but it might be more likely, see [1][2].

Figure 3: A network that is not tree-sibling (the red node does not have a non-reticulate sibling).

Reticulation-visible
From every reticulation node there is a path to some leaf or cut-arc (a branch whose removal disconnects the network) such that this path does not pass through any reticulations. This is another attempt to weaken the tree-child restriction, thus obtaining a larger class of networks for which many computational problems are still tractable. It is incomparable with tree-sibling (a reticulation-visible network does not have to be tree-sibling and vice versa) but this class clearly contains the class of tree-child networks, and in fact is much larger. It does not forbid all invisible nodes, but just invisible reticulation nodes. It has been shown in the book by Huson, Rupp and Scornavacca that the so-called Cluster Containment problem becomes tractable for reticulation-visible networks. If the same is the case for the Tree Containment problem is still an open question.

Figure 4: A network that is not reticulation-visible. The red reticulation node is not "visible".

Galled trees
All reticulation cycles are disjoint. Introduced by  Gusfield, Eddhu and Langley [6] although studied before under different names. Makes computational problems much easier but seems biologically unrealistic. On the other hand, galled trees could have a future in the context of data-display networks, by using the galls to show where the reticulate activity is in the network, rather than claiming that each gall represents exactly one reticulation event.

Galled networks
Each arc leaving a reticulation node is a cut-arc. Introduced by Huson and Klöpper [7] (who gave a different but equivalent definition) as a generalization of galled trees, giving a fast algorithm for constructing galled networks from clusters. Hasn't been studied much since. (Be aware that there is also an article using "galled network" as an alternative term for galled tree.)

Figure 5: A network that is not a galled network. The red arc leaves a reticulation node but is not a cut-arc.

Level-k (not a restriction, but a measurement)
Also a generalization of galled trees (which are basically level-1 networks). Every network is a level-k network for some k. Hence, “level-k” should not really be viewed as a topological restriction, but rather as a measure of how “tangled” (intensely concentrated) the islands of reticulation are in the network. The higher k is, the more tangled the network is; level-0 networks are simply trees. For more information, see a previous blog. Other proposed measurements of tangledness include k-nested, r-reticulation and depth-k.

Regular and normal
If you see a phylogenetic network as a representation of a set of clusters, then it makes sense to consider regular networks (introduced by Baroni, Semple and Steel). A network is regular if it is the so-called "cover digraph" (Hesse diagram) of its set of clusters. Hence, for each set of clusters, there exists a unique regular network with precisely that set of (hardwired) clusters. Normal networks have the additional requirement of being tree-child, thus forming a very restricted class of networks. For example, the network in Figure 1 is not regular and hence also not normal.

DAG or tree-with-edges-added?
This is a rather subtle one. If one views a phylogenetic network as a tree with edges added, then this leads to a different space of networks than the “a phylogenetic network is essentially a directed acyclic graph” definition encountered in other articles. The point being that if you insist that a network has to be “grown” from some tree starting point (by adding edges in a certain way), certain topologies cannot be reached which can be reached if the we do not anchor it in this way. The following figure shows an example.

Figure 6: A network that cannot be obtained by adding edges to a tree (for common edge-adding rules).

It can be shown that any tree-sibling network can be constructed by adding edges to a tree, but the network in Figure 3 shows that the converse is not true (the shown network can be constructed by adding edges to a tree, but is not tree-sibling). 

This restriction touches on the fundamental question whether there exists something like a species tree, and if it might be possible to reconstruct this species tree before starting network analysis.

A related but stronger (?) restriction was recently used by Wu [9]. In his RECOMB 2013 article, he writes “(R1) For a network N, when only one of the incoming edges of each reticulation node is kept and the other is deleted, we always derive a tree T'.”

Conclusion
We see from this list that there are already some quite different topological properties and restrictions in circulation for rooted phylogenetic networks. To biologists these discussions might appear to be a strange side-show to keep computer scientists in work. But it runs deeper than that, because it touches on three fundamental issues. Firstly, what are we trying to model exactly? Secondly, the importance of understanding the networks that your favourite software for constructing rooted phylogenetic networks will not build, however biologically relevant, due to the fact that they are a priori excluded from its search space. Finally, since the total number of networks is huge, it could be inevitable to focus on certain restricted classes of networks when one wants to search through network-space efficiently.

Note: There is a follow-up post Topological restrictions: some comments.

REFERENCES

[1] Miguel Arenas, Mateus Patricio, David Posada and Gabriel Valiente. Characterization of Phylogenetic Networks with NetTest. In BMCB, Vol. 11:268, 2010. 

[2] Miguel Arenas, Gabriel Valiente and David Posada, Characterization of Reticulate Networks Based on the Coalescent with Recombination, Mol Biol Evol (2008) 25 (12):2517-2520.

[3] Mukul S. Bansal, Eric J. Alm, Manolis Kellis, Reconciliation Revisited: Handling Multiple Optima when Reconciling with Duplication, Transfer, and Loss, RECOMB 2013.

[4] Gabriel Cardona, Merce Llabres, Francesc Rossello, Gabriel Valiente, The comparison of tree-sibling time consistent phylogenetic networks is graph isomorphism-complete, arXiv:0902.4640 [q-bio.PE], 2009.

[5] Gabriel Cardona, Mercè Llabrés, Francesc Rosselló and Gabriel Valiente. A Distance Metric for a Class of Tree-Sibling Phylogenetic Networks. In BIO, Vol. 24(13):1481-1488, 2008.

[6] Dan Gusfield, Satish Eddhu and Charles Langley. Efficient reconstruction of phylogenetic networks with constrained recombination. In CSB03, Pages 363-374, 2003.

[7] Daniel H. Huson and Tobias Klöpper. Beyond Galled Trees - Decomposition and Computation of Galled Networks. In RECOMB 2007, Vol. 4453:211-225 of LNCS.

[8] Leo van Iersel, Charles Semple and Mike Steel, Locating a Tree in a Phylogenetic Network, Information Processing Letters, 110 (23), pp. 1037-1043 (2010).

[9] Yufeng Wu. An Algorithm for Constructing Parsimonious Hybridization Networks with Multiple Phylogenetic Trees. RECOMB 2013.

Posted by in Acyclic graph, Directed graph, Level-k network, Limitation, optimization criteria

Permalink