Posted by: David Morrison
Tattoo Monday XVIII
We haven't had any Charles Darwin tree tattoos on this blog for quite a while, so here is a new collection of Darwin's best-known sketch from his Notebooks (the "I think" tree) — for other examples, see Tattoo Monday III, Tattoo Monday V, Tattoo Monday VI, Tattoo Monday IX, and Tattoo Monday XII.
Tattoo Monday XVIII
We haven't had any Charles Darwin tree tattoos on this blog for quite a while, so here is a new collection of Darwin's best-known sketch from his Notebooks (the "I think" tree) — for other examples, see Tattoo Monday III, Tattoo Monday V, Tattoo Monday VI, Tattoo Monday IX, and Tattoo Monday XII.
Which airlines serve the best wine?
I have only flown Business Class once, when I got upgraded on a flight from Sydney to Auckland; and I have never flown First Class. So, I don't really care about the so-called Cellars in the Sky, because I get only the vin ordinaire in Economy Class.
However, some people do care about the quality of the beer, wine and spirits served to the high flyers. These include the people at Business Traveller magazine / web site. For more than 30 years, they have handed out annual Cellars in the Sky awards, after evaluating the quality of the wine served to business class and first class passengers on the world's airlines.
Airlines can choose to enter the Awards process provided that they serve wine in business or first class on mid- or long-haul routes. The airlines submit up to two red wines, two white wines, a sparkling wine, and a fortified or dessert wine, from both their business and first class cellars. These wines are assessed and scored (blind) by a panel of independent judges. The awards are based on the average marks for the wines concerned, with separate awards for First Class and Business Class, plus an Overall Award for consistency across both classes.
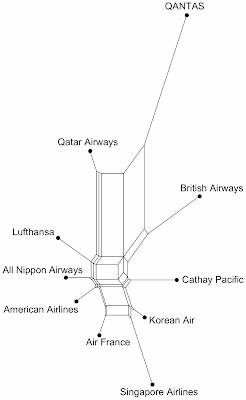
I have analyzed the data for the Best Overall Cellar for the years 2006 to 2018, inclusive. The number of airlines commended each year varied from 3 to 5 (average 4.0). I simply gave each airline a score scaled from 0–1 depending on its ranking in the awards list. There were 16 airlines mentioned over the 13 years, but I have included only those 10 that appeared in more than one year.
Since these are multivariate data, one of the simplest ways to get a pictorial overview of the data patterns is to use a phylogenetic network, as a tool for exploratory data analysis. For this network analysis, I calculated the similarity of the airlines, based on the awards they received, using the manhattan distance, and a Neighbor-net analysis was then used to display the between-airline similarities.
The resulting network is shown in the graph. Airlines that are closely connected in the network are similar to each other based on when they won their awards, and those airlines that are further apart are progressively more different from each other.
Only one airline received an award in every year: QANTAS, followed by Qatar Airlines with 9 out of 13 years. These two airlines are grouped together at the top of the figure. The other airlines are arranged based on which years they won awards. For example, Cathay Pacific won 7 awards, and both Singapore Airlines and British Airways won 5, but they were mostly not in the same years. American Airlines, Air France, Korean Air and Lufthansa each won only 2 awards.
So, if you want to get your money's worth out of your business-class ticket, then it would be a good idea to try QANTAS or Qatar Airlines — the hours will pass more quickly with a glass of good wine in your hand.
Posted by in Exploratory data analysis
Corals — a new metaphor for phylogenetic diagrams
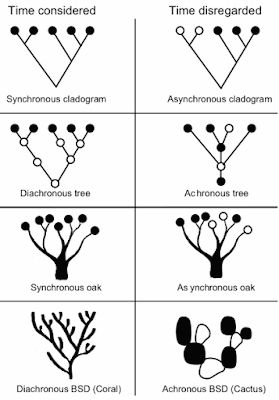
A year ago I mentioned a published discussion of the different branching diagrams that have been used for phylogenetic relationships (Tree metaphors and mathematical trees). If we consider the form of the relationship and whether time is involved, we get the following four possible diagram types:
Most current phylogenetic diagrams claim to show sister-group relationships (which means that ancestors are inferred only), with a time-order to the branching sequence. There is a broad range of diagram types in use, both mathematical and metaphorical. For example, the top four in this next diagram are mathematical and the bottom four are metaphorical variants of the above 2x2 table:
The connection between these different diagrams has both conceptual and practical problems, although these seem to be overlooked by most practitioners. This issue as been addressed by János Podani in a paper that is now online:
The Coral of Life. Evolutionary Biology (2019).To quote from the Abstract:
The Tree of Life (ToL) has been of central importance in the biological sciences, usually understood as a model or a metaphor, and portrayed in various graphical forms to summarize the history of life as a single diagram. If it is seen as a mathematical construct — a rooted graph theoretical tree or, as more recently viewed, a directed network, the Network of Life (NoL) — then its proper visualization is not feasible, for both epistemological and technical reasons. As an overview included in this study demonstrates, published ToLs and NoLs are extremely diverse in appearance and content ... Metaphorical trees are even less useful for the purpose, because ramification is the only property of botanical trees that may be interpreted in an evolutionary or phylogenetic context. This paper argues that corals, as suggested by Darwin in his early notebooks, are superior to trees as metaphors, and may also be used as mathematical models. A coral diagram is useful for portraying past and present life because it is suitable: (1) to illustrate bifurcations and anastomoses, (2) to depict species richness of taxa proportionately, (3) to show chronology, extinct taxa and major evolutionary innovations, (4) to express taxonomic continuity, (5) to expand particulars due to its self-similarity, and (6) to accommodate a genealogy-based, rank-free classification.It is worth checking out this paper, even if only for the new Coral of Life diagram that is presented in its Figure 3, which synthesizes much of our current knowledge.
Tournament success is not poker success
Let us suppose for a moment that we wish to list the world's best professional poker players. This might be of some interest, because poker is partly a game of luck (the cards are dealt at random) and partly a game of skill (players choose how to play their cards). Indeed, put simply, the idea is to convince your opponents that you have a weak hand when they have a strong one (so that they will bet against you) and a strong hand when they have a weak one (so that they will fold).
One well-known way to assess poker success is to look at tournament winnings. Indeed, Nathan Williams recently did this for The Top 50 Best Poker Players of All Time by simply listing the 50 greatest money earners from The Hendon Mob database. This database accumulates data on the lifetime money winnings for all of those participants who have ever cashed in a live poker tournament.
However, this approach does not work. In fact, there are at least five reasons why this is not appropriate:
- Inflation continues unabated. After all, $1 now is not worth as much as $1 was 30 years ago. In fact, something that cost $1 in 1990 would cost a bit more than $2 now (ie. the money has been devalued to 50%). So, the value of current winnings cannot be compared to those of the past.
- There are more tournaments now than there have ever been. So, there are more opportunities to play them now, and to thereby potentially accumulate more money for the same tournament success rate.
- The tournament fields are now generally bigger. This means that the average prize money for each tournament is now much greater than before (since the money is provided by the participants themselves). In particular, the top prizes now provide more money than whole tournaments did 20 years ago.
- Some of the best players play online rather than live. Obviously, this is a bit more difficult these days, due to the banning of online poker in the USA, but it is still a significant source of poker income for many people.
- Some of the best players do not play many tournaments —instead, they play cash games. Indeed, if you want to make a living playing poker, you may be better off playing for cash rather than for prize money, as tournament success is much more of a lottery.
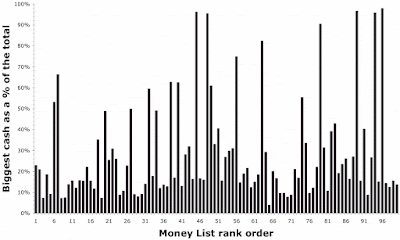
Note that for the majority of players, a large part of their lifetime winnings came from a single tournament — the median percentage is 18.4% (range 3.8–97.7%). Indeed, for some of the players it is >50%, and for a few it is almost all of their money. Bigger fields mean more money per tournament, and thus bigger cashes when you do well. Note, incidentally, that this graph does contain the top 17 biggest cashes in history (to date).
An alternative approach
So, in order to evaluate players, we actually need a list of criteria that is independent of money won. That is, we need a list of the poker skills of each player. There are several different skills involved in playing poker, and presumably some people are good at some of them, and other people are good at some of the others. A comparison of relative skills is what we need.
This approach was actually tried by Barry Greenstein back in c. 2005. What he did was try to rate a group of 33 of the poker players that he had played against in cash games. He rated these players by style of play, based on ten playing criteria (each scored on a 1–10 scale):
- Aggressiveness
- Looseness
- Short-handed play
- Limit poker
- No-limit poker
- Tournaments
- Side games
- Steam control
- Against weak players
- Against strong players
Greenstein himself notes: "I don’t think you can add up the ratings in the skill categories to get an accurate comparison of players." He is right; but first let's do it anyway. So, the next graph shows the total score (out of 100) for each player. (Click on the figure to see it at full size.)
This problem here is that we are comparing apples with oranges. That is, the rank ordering of the sum does not make much sense, because it does not group players with similar playing strengths. The rank order would make sense when comparing each feature one at a time, but not for the total. For example, ranking by total winnings does make sense, because we have only one criterion: money (although it is not a useful criterion). This is the basic weakness of having a single rank order.
As one example of how the "overall score" misses important points, note that Eric Seidel and John Juanda have the same total. However, Seidel exceeds Juanda on Stem control, while Juanda exceeds Seidel on Looseness — these are actually two rather different players.
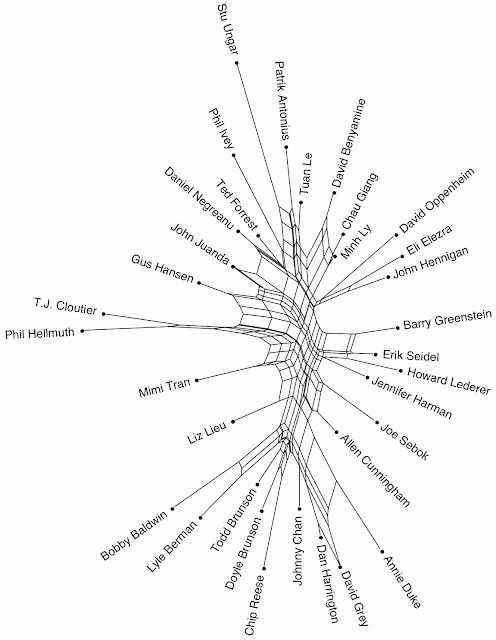
A better way to look at the data is to use a network, as we often do in this blog. The final graph is a NeighborNet (based on the manhattan distance) of Greenstein's data. Each point represents one of the 33 people. Those people that are near each other in the network have a similar set of scores, while people further apart are progressively more different from each other as poker players.
As you can see, there is no simple trend from "best" to "worst", but instead a complex set of relationships, just as we would expect. However, the network does show an overall trend of decreasing total score from top to bottom (compare this to the previous graph).
Note, first, that Eric Seidel and John Juanda are on opposite sides of the network (Juanda left, Seidel right). This illustrates how much better the network is as a display of the data, compared to simply summing the scores (as in the previous graph). The network accurately shows the differences in the relative playing styles.
There are some players who are actually gathered together in the network, indicating that they have similar scores across all 10 criteria. For example, Barry Greenstein , Eric Seidel and Howard Lederer rarely differ by more than 1 point on any of the criteria — according to Greenstein, these people have very similar playing styles.
Alternatively, Pil Helmuth and T.J. Cloutier have scores that differ from the other players — both have low scores on Side games and Steam control. Gus Hansen is near these two because all three have high scores for Against weak players. Similarly, the legendary Stu Ungar and Patrik Antonius both have high Aggressiveness and Looseness.
There is one a final point worth mentioning. As Michel Bettane once said (The absurdity and flattery of scores):
It doesn't take a genius to appreciate the absurdity of giving a number score to a work of art or, worse still, an artist. Salvador Dalí had huge fun scoring great artists (including himself) on the basis of design, color, and composition — but that says far more for his sense of provocation and irony than it does for the principle itself.Is poker an art, a science or a sport? If it is either of the first two, then scoring players may actually be a Bad Idea.
The Tree of Life (April 1)
The so-called Tree of Life is actually an anastomosing plexus rather than a divaricating tree, due to extensive interconnections between the cell and genome lineages during early single-cell evolution. These connections may have been caused by the process known as horizontal gene transfer.
Furthermore, the alleged Last Universal Common Ancestor may not have been a single coherent group, but may have been a mixture of quite different genotypes. After all, this supposed ancestor does not represent the origin of life, but was itself the end-product of an extensive prior evolutionary history.
These two basic points are illustrated in the following figure.
Happy April 1. For previous posts, see:
Posted by in Gene flow, Phylogenetic tree, Visualization
Which US cities are best for walking, biking and public transport?
In the modern world, there is a lot of discussion about the environmental damage caused by cars and trucks, not least due to their involvement in global climate change. The pro-active parts of this discussion revolve around banning cars, so that parts of cities and towns can return to pedestrian areas (eg. Life in the Spanish city that banned cars; The automotive liberation of Paris), and encouraging alternative modes of transport, particularly bicycles (eg. Copenhagenize your city: the case for urban cycling; Britain wants cycle-friendly cities).
In particular, some cities throughout the world are taking active steps to improve the "walkability" of their centers, including Addis Ababa, Auckland, Denver, Hanoi, London, Manchester and San Francisco (What would a truly walkable city look like?), and the "cyclability" of their inner suburbs, including Calgary, Copenhagen, Eindhoven, Lidzbark, Purmerend, San Sebastian, Utrecht and Vancouver (Top 10 pieces of cycling infrastructure: which country does it right?). On the other hand, there are some cities who have not yet tried to do much about cycling, including Beijing, Cairo, Delhi, Hong Kong, Moscow, Mumbai, Nairobi, Orlando, São Paulo and Sydney (Top 10 worst cities for cycling ).
The USA is not usually considered to be at the forefront of this movement, having long ago wedded itself to the cult of the private motor car. However, this does not mean that US cities are all the same in terms of non-car transportation. For example, the Walk Score site, which is part of the Redfin real estate organization, provides a ranking of all US cities and neighborhoods with a population of 200,000 or more, in terms of how friendly they are for: walking, biking and transit.
The ranks are based on a score out of 100 for each location, using various methodologies:
— Walk Score analyzes hundreds of walking routes to nearby amenities; points are awarded based on the distance to amenities in each category.Our interest here is in combining these three pieces of information into a single picture, showing which cities are generally good, at the moment.
— Bike Score is calculated by measuring bike infrastructure (lanes, trails, etc), hills, destinations and road connectivity, and the number of bike commuters.
— Transit Score assign a "usefulness" value to nearby transit routes based on their frequency, type of route (rail, bus, etc), and distance to the nearest stop on the route.
Not unexpectedly, the Walk Score and Transit Score are highly correlated (86% shared rankings), while the Bike Score is not as highly correlated with either of these (49% and 42%, respectively). This means that the same cities tend to be good for the first two criteria. The three best cities for the Walk Score are New York, Jersey City and San Francisco, while the top two for the Transit Score are New York and San Francisco. On the other hand, for the Bike Score the top two are Minneapolis and Portland — it would be difficult to imagine either New York or San Francisco as being good for biking!
If we define a "good" score as being >70, then only San Francisco has a score for all three criteria >70, although Boston comes close. On the other hand, Pittsburgh and Washington D.C. have the most consistent scores across the board, because they have uniformly middle-rank scores.
Since these are multivariate data, one of the simplest ways to get a pictorial overview of the data patterns is to use a phylogenetic network, as a tool for exploratory data analysis. For this network analysis, we calculated the similarity of the cities using the Manhattan distance, and a Neighbor-net analysis was then used to display the between-city similarities.
The resulting network of the 98 cities with complete data is shown in the figure. Cities that are closely connected in the network are similar to each other based on how good they are for walking, biking and transit, and those cities that are further apart are progressively more different from each other. The color-coding for the cities is from Megaregions of the United States.
The network generally shows decreasing walking / transit scores from top to bottom, and decreasing biking scores from right to left. We have labeled only the top group of 29 cities, which are distinctly "better" than the remaining 69, plus four unusual cities (at the middle-left).
Note that, as expected, New York, San Francisco and Boston stand out at the top of the network. Note, also, that Minneapolis and Portland are separated in the network from the other cities, because of their high Bike Scores — all of the other cities in the top group have much lower biking scores. Newark, in particular, has a low biking score. New Orleans is at the bottom-left of this group because it has a low Transit Score but not Walk Score.
For the four unusual cities, separated at the left of the bottom group: Dallas has a low Transit Score, and Atlanta, Cincinnati and San Diego all have a low Bike Score.
The city at the very bottom-left of the network, which has the lowest score on all three criteria, is Arlington TX. Along the same lines, there is an online graph of The 10 most dangerous states for cyclists, showing Florida way out in front.
Finally, you should be warned about potential problems with rankings like these, based on only a few selected criteria. For example, the real estate site StreetEasy recently tried to compile a list of the 10 Healthiest Neighborhoods in New York city, and ended up listing the Brooklyn industrial area of Red Hook as number 1, which engendered a couple of negative comments, such as:
I guess the fact that the majority of Red Hook’s parkland has been closed for many years due to lead contamination, or the fact that we have one of the highest asthma rates in the city, was overlooked for this study.Caveat emptor!
Tattoo Monday XVII
Here are seven more tattoos in our compilation of evolutionary tree tattoos from around the internet. For more examples of the circular design for a phylogenetic tree, in a variety of body locations, see Tattoo Monday V, Tattoo Monday VII, Tattoo Monday X and Tattoo Monday XI.
At the bottom of this post is an unusual linearized version of this same type of tree.
A network analysis of basic leisure-time activities
Social scientists like to compile information about what human beings do with their time, day and night. Some of that time is called "work time", where we often have little control, and the rest is "leisure time", during which we have at least some control over the time we spend on each activity. This blog post looks at how much time people in different countries allocate to some of their different leisure-time activities.
The data are taken from the American Association of Wine Economists' Facebook page: Leisure Time Spent in OECD Countries. The five leisure-time activities included in the dataset are:
- Eating & drinking
- TV & radio
- Sports
- Shopping
- Sleeping
Since these are multivariate data, one of the simplest ways to get an overview of the data patterns is to use a phylogenetic network, as a tool for exploratory data analysis. For this network analysis, I first normalized the data within each of the five activities, and then calculated the similarity of the countries using the Manhattan distance. A Neighbor-net analysis was then used to display the between-country similarities.
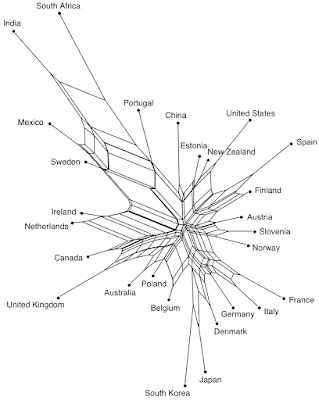
The resulting network is shown in the first figure. Countries that are closely connected in the network are similar to each other based on the relative times allocated to the leisure-time activities, and those countries that are further apart are progressively more different from each other.
Clearly, there is considerable diversity between the countries. Moreover, there is very little in the way of consistent patterns in the network — it is basically a single "starburst" pattern. So, we may first conclude that the people of the different countries basically all go their own way, when it comes to allocating their leisure time.
Some of the network associations may result from historical or cultural similarities, such as the closeness of Japan and South Korea in the network. However, this clearly does not apply in other cases — for example, Spain and Portugal are not near each other, and neither are Australia and New Zealand, nor are Denmark, Norway and Sweden. Cultural generalizations seem therefore not to be supported by the data.
India and South Africa both stand out from the rest of the network, indicating that their people behave differently to all of the other countries (on average). Notably, both countries have very short times allocated to Sports and to Shopping. India also has rather short TV/radio time and a long Sleeping time, while South Africa has the longest Sleeping time of all of the countries (45 min longer than the country average!).
The USA has relatively short Eating/drinking time, a long Sleeping time, and the longest TV/radio time of all. That is, Americans spend less time on eating & drinking than most other people, and use the time gained for watching TV and sleeping, instead.
Of the other countries, France has the longest time spent on Eating/drinking, followed by Denmark and Italy, and then Japan and South Korea. Canada and the United Kingdom, on the other hand, actually have the shortest Eating/drinking times of all of the countries. Spain has a relatively short Eating/drinking time and the longest time of all allocated to Sports (nearly double the country average!). This may be a more healthy way to behave than the American one.
A related topic that we could look at is gender differences in time allocation, and how this may differ between countries. The data for this are taken from another American Association of Wine Economists' Facebook page: Time per Day Spent Eating and Drinking, by Country and Gender.
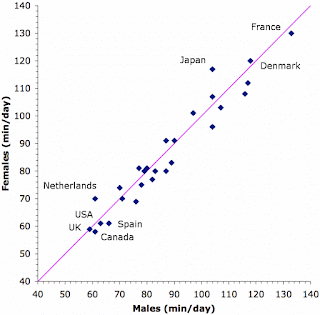
So, the country data are for the averages for Eating/drinking only, with separate observations for males and females. These two averages are plotted against each other in the second figure, where each point represents a single country. I have labeled the three top countries and the five bottom countries.
Obviously, there is a close correlation between the males and females within any one country, so that most of the time variation is between countries (93%). If couples and families usually eat together, then this result is to be expected. It is the children who are likely to have more independent eating habits!
However, there are 14 countries where the average male time somewhat exceeds that for females, and only 7 where the female average time exceeds that for the males, with the remaining 6 being approximately equal (as represented by the pink line). Interestingly, the 2 biggest deviations from equality are where females spend more time on Eating/drinking than do the males (Japan and the Netherlands). You may make of this what you will.
* The 12 missing OECD countries are:
Chile, Czechia, Greece, Hungary, Iceland, Israel, Latvia, Lithuania, Luxembourg, Slovakia, Switzerland and Turkey.
A question about coalescent-based species phylogenies
This may be a naive question; but as I am now semi-retired, so I can now ask it without professional embarrassment.
It is common when constructing species phylogenies (both trees or networks) to use a model that takes into consideration multiple replacements of characters through evolutionary time. If the states of any given character have been modified multiple times, then the currently observed differences in that character between taxa will not accurately reflect their evolutionary history.
For example, we "correct for multiple substitutions" when using DNA/RNA sequence data. We do this because, with only four character states, the probability that undetectable multiple substitutions have occurred increases considerably through evolutionary time. So, we have developed any number of sophisticated models for addressing this issue, such as JC and GTR; and it is unusual to see a published paper with a species phylogeny that does not use one of them.
This leads to a question about population phylogenies. In this case, the use of the coalescent model is prevalent. It allows the calculation of various population parameters, based on viewing phylogenies backwards through time. For the purpose of phylogenetics, the key calculation is the coalescence time of each pair of lineages, although population size is also of some interest.
The coalescent model is based on a set of assumptions, of course. Indeed, it is based on the Fisher-Wright model of population genetics. This is an infinite-sites model, meaning that it assumes that multiple replacements of characters do not occur during the evolution of the populations. That is, if the genetic sequences are infinitely long then the probability of multiple substitutions is 1 / infinity = zero.
This, then, is my question: Can we really assume that multiple substitutions never occur, in one part of the analysis, and assume that they are so common that we need to adjust for them, in another part of the same analysis?
I have not found this issue addressed either in the published literature or on the internet. Indeed, most people I have spoken to did not even realize that the coalescent is ultimately based on an infinite-sites model. So, for me at least, this is an interesting question.
Posted by in Coalescent, phylogeny